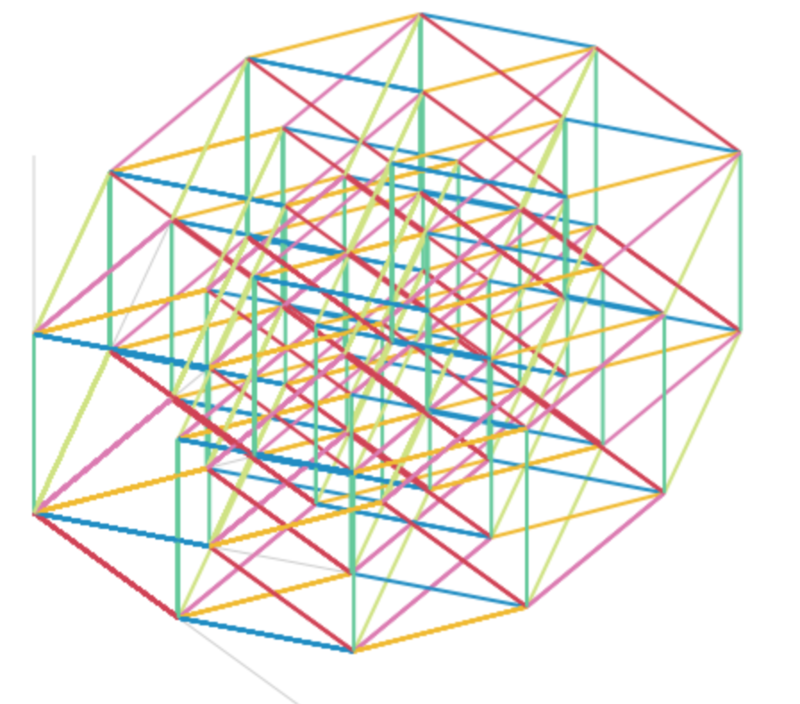
先日の記事で触れたように、次元数の軸が、どれかの次元の軸についての方程式になっていた場合どんな挙動になるのかの実験のためにn次元単位立体を描画するプログラムを書いています。プログラマだと実験の道具を自分の指先でちょちょいと作れてとても便利。
今日の夕方にJSFiddleで暇つぶしに書いていたら、n次元(0含む)の立方体の辺を描画するものが呆気ないほど簡単にできてしまいました。
超立方体 - Wikipedia
正八胞体 - Wikipedia
5次元立方体のワイヤフレーム。コード末尾の方のstateのdが次元数(軸の数)。"Edit in JSFiddle"から、この数値を変えたりして実験できます。
gistはココ: gist: Draw n-dimentional cube on canvas.
あくまでスクリプト的なコードで、効率などは無視していますが、わりかしシンプルに表現できました。
仕組みとしては、
- x軸の角度と、y軸の角度をパラメータとして受け取って、この2軸が作る角度を等分割して残りの軸を割り当てる。
- 次元軸の置換(permutation)について、 これと
{0: 1, 1: 1, ..., n: 1}なベクタでplotVertexを呼ぶ。 plotVertexは座標ベクタを舐めて、各スカラーxについて半径xの円周と軸の交点に向けて辺を描画する。この交点を保存しておいて、次の辺のスタート地点とする。
という、定規とコンパスを使う時と全く同じ仕組みになっています。
出来上がった図形は、立体を2次元に投影するときに、互いに直角ではない角度を直角であると錯覚するのと全く同じように、全ての角度が直角であると錯覚して見る必要があります。
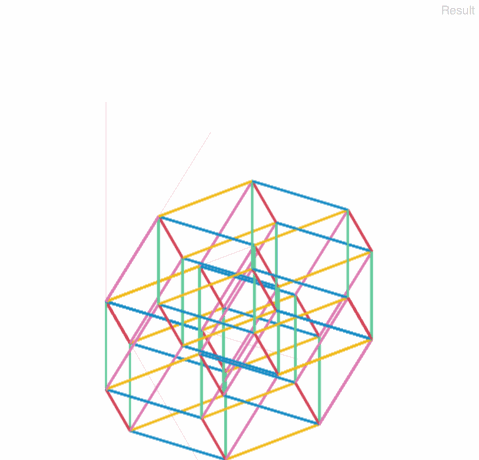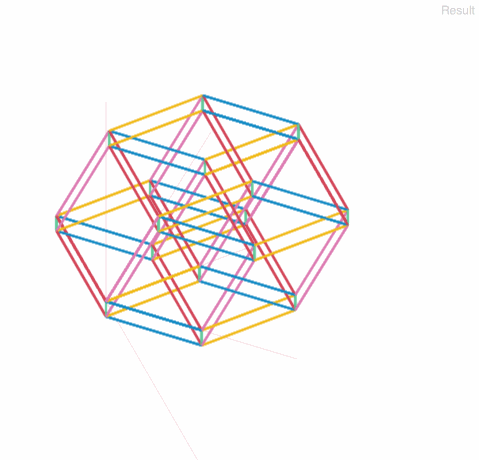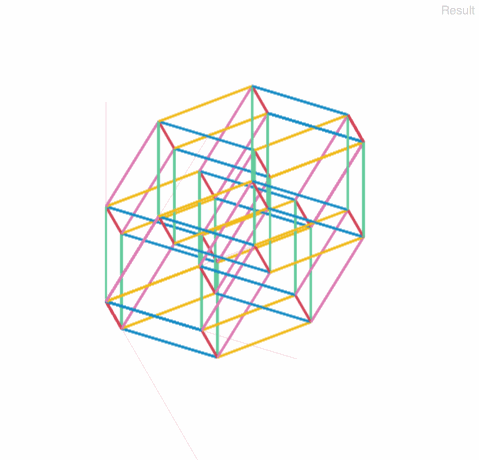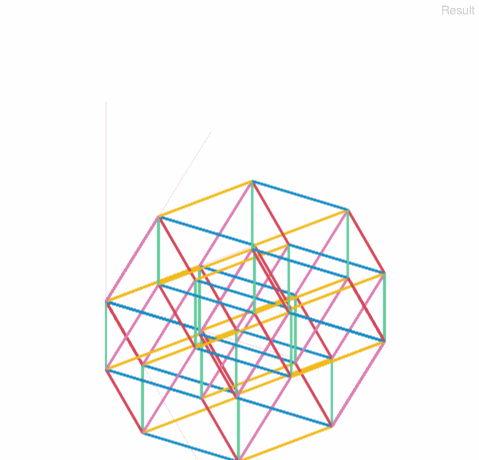
以下ギャラリーです。辺の重なりの奥-手前関係は考慮していないので注意。
2次元立方体 2-cube
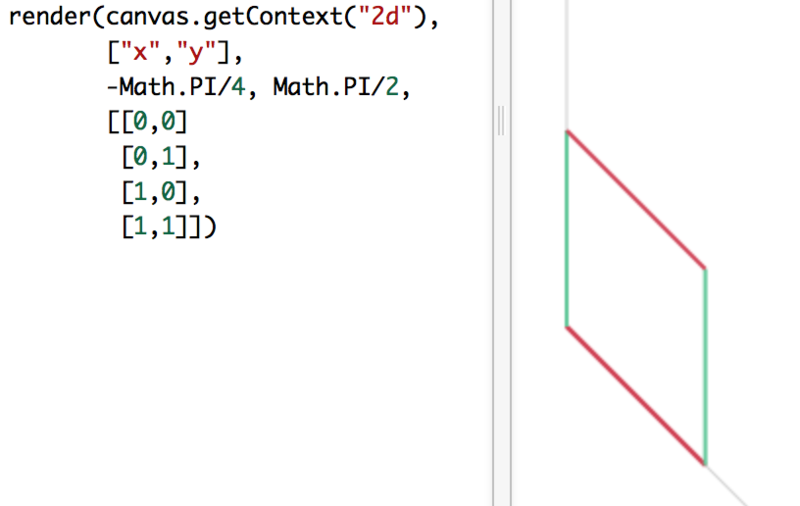
3次元立方体 3-cube
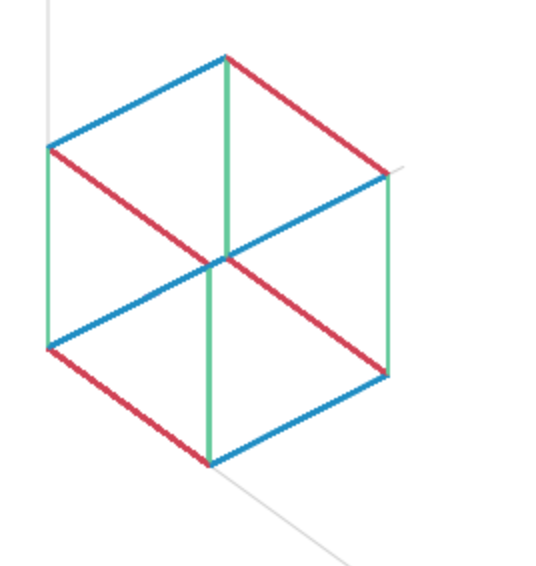
4次元立方体 4-cube

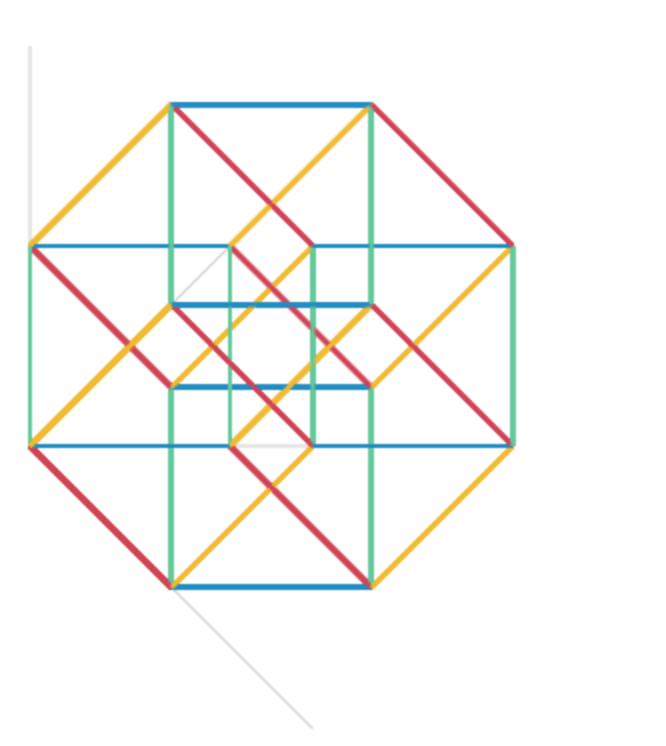
5次元立方体 5-cube

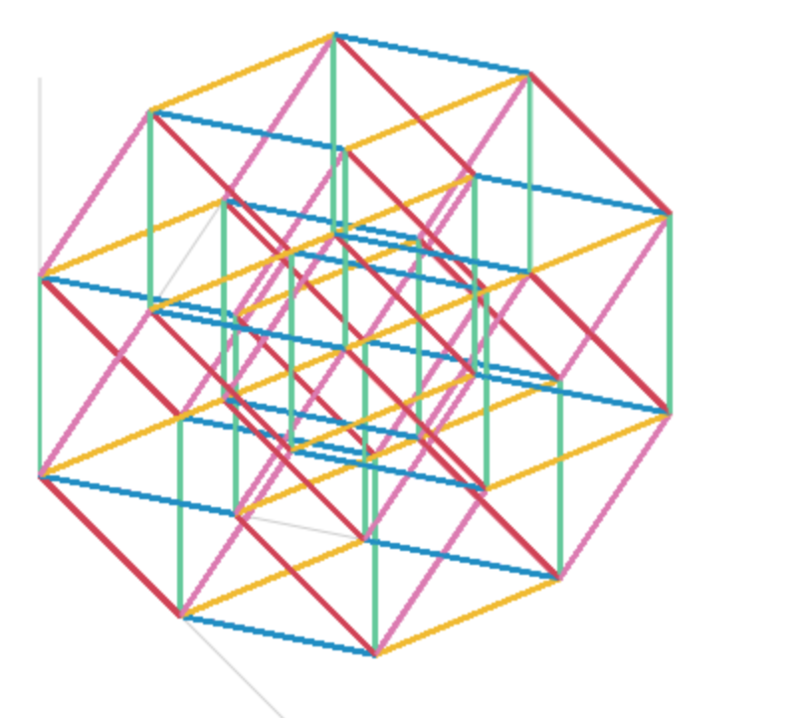
6次元立方体 6-cube


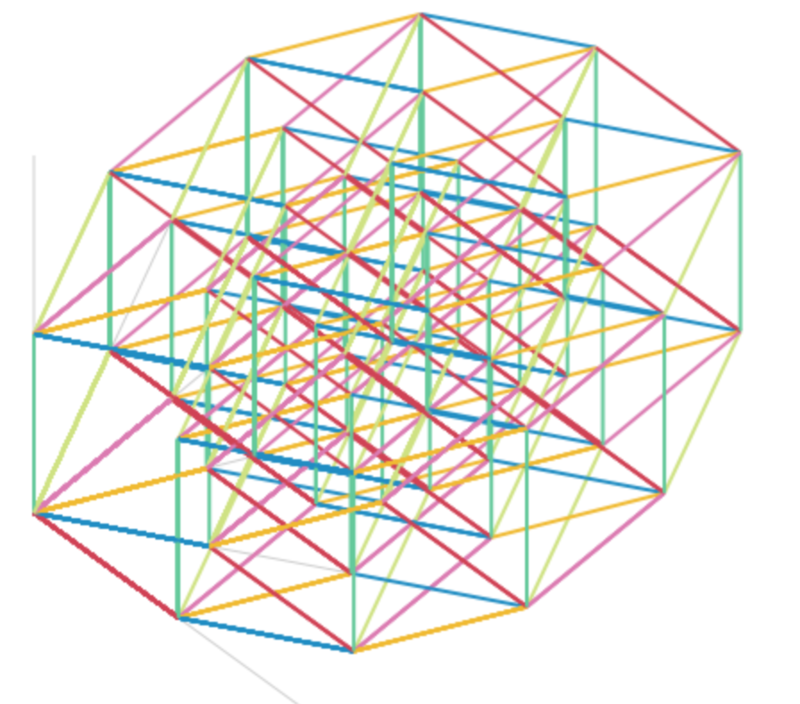
7次元立方体 7-cube

8次元立方体 8-cube

9次元立方体 9-cube
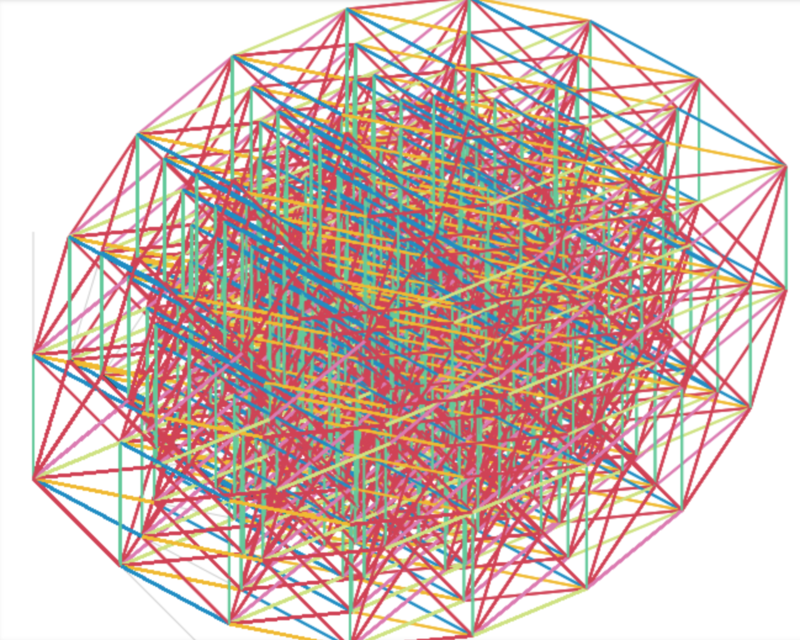
ちゃんと各頂点に次元数本の辺が集まっているのが確認できます。
次元が増えるにつれて赤くなっていくのは、色を設定し忘れた軸方向の線が、デフォルトの赤で引かれているからです。
暇を見つけて改良していきます。任意の軸についての回転を実装すればだいぶ把握しやすくなりそう。
編集履歴
Apr 18 2015
- もっとうまいやり方を思いついたのでコードを修正しました。美しくなったけどネストした再帰のせいで重くなった。
Apr 19 2015
コードを修正して、軸を、等分割位置から0.1τずらすようにしました。ちょうど重なって繋がっているように見えていた線分がうまいことズレて見れるようになった。
任意の軸方向にスケールできるようにしました。